| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- jupytertheme
- 주피터노트북 커널 추가
- 경사하강법
- lol api
- overfitting
- 데이터분석
- GitHub
- regression
- deeplearning
- 주피터 노트북 테마
- 한빛미디어
- Udacity
- 주피터노트북
- feature scaling
- 모두를 위한 딥러닝
- 주피터테마
- Machine Learning
- 딥러닝
- 회귀분석
- random forest
- MySQL
- 주피터노트북 커널 목록
- 나는리뷰어다2021
- deep learning
- Python
- 주피터노트북 커널 제거
- Linear Regression
- pandas
- ubuntu
- Git
- Today
- Total
유승훈
Intro to machine learning - (6) Regression(2) 본문
Intro to machine learning - (6) Regression(2)
seunghuni96 2021. 1. 15. 15:18앞선 글에서 이어집니다.
Intro to machine learning - (6) Regression(1)
이번 챕터는 회귀분석에 대한 내용입니다. 보충이 필요한 내용은 학교에서 들었던 회귀분석 강의 내용을 첨부했습니다. 이전 강의에서 배웠던 알고리즘들이 이산형 Y 문제를 푸는 것들이었습니
seunghuni96.tistory.com

두 그래프에 있는 회귀식(회귀선)의 성능은 비슷해보여도, 큰 차이가 있습니다.
앞서 언급했던 SSE로 비교를 해 보면, 왼쪽보다 오른쪽 그래프의 SSE가 더 큽니다. 데이터가 많기 때문에 실제 데이터와 회귀식으로 예측한 값의 차이의 제곱합을 계산할 때, 경우의 수 자체가 커지기 때문입니다.
이처럼 SSE는 단순히 데이터가 많아질 때 값 자체가 커진다는 단점을 갖습니다. 일반적으로 SSE가 비교적 큰 모델은 성능이 좋지 않다는 것을 의미하는데, 위의 두 그래프를 비교했을때는 성능에는 크게 차이가 없어보입니다.
따라서 SSE뿐 아니라 R-Squared라는 평가지표도 활용합니다.
$R^2 = 1-\frac{SSE}{SST} = \frac{SSR}{SST}$
총 변동인 SST 중에서, 회귀식으로 설명되는 변동인 SSR의 비율을 계산합니다. SST=SSR+SSE이기 때문에 총 변동 중 회귀식으로 설명되지 않는 변동의 비율을 1에서 빼주는 방식으로 구할수도 있습니다.

R-Squared는 0에서 1 사이의 값을 갖습니다. SSR, 즉 독립변수(X)의 변동이 종속변수(Y)의 변동을 얼마나 설명하는가를 의미합니다. 당연히 R-Squared 값이 작으면 우리의 회귀선이 데이터의 트랜드를 잘 캐치하지 못하고 있는 것을 의미하고, 크면 회귀모델의 독립변수들이 종속변수의 변동을 잘 설명하고 있다는 것을 의미합니다.
하지만 R-Squared 또한 100% 믿을 수 있는 Metric은 아닙니다. 변수의 영향력에 따른 차이는 있지만, 독립변수가 추가되면 R-Squared도 계속해서 커진다는 단점을 갖습니다. 이 단점을 보완하는 Metric으로 Adjusted R-Squared가 있습니다.
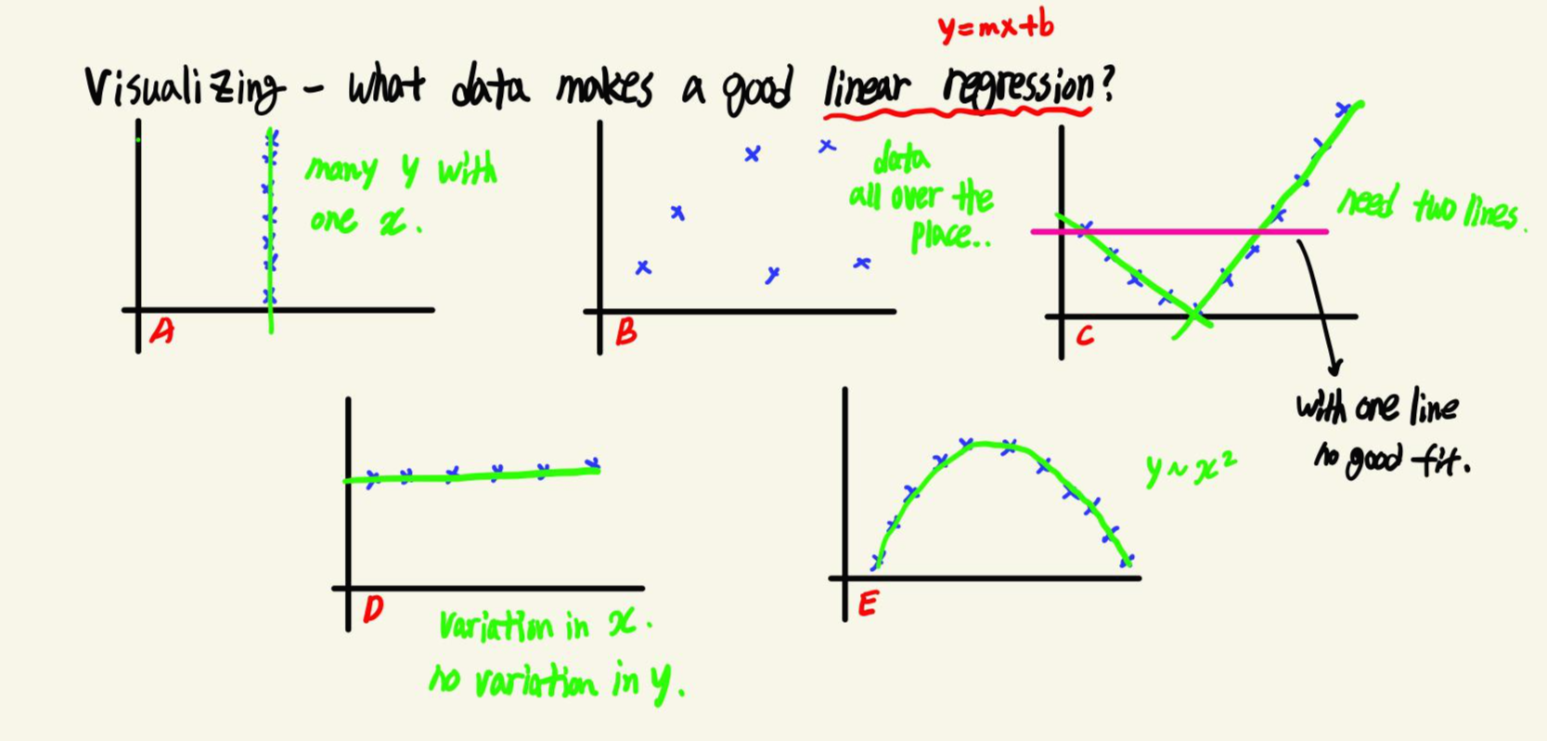
강의에서는 우리가 만든 회귀모델을 시각화하는 것의 중요성에 대해서도 이야기합니다. 여러 데이터 중에 Linear Regression으로 설명하기 좋은 데이터는 무엇일까요? 각 Plot을 살펴보면,
A - 동일한 X값에 대해 너무 많은 Y가 존재합니다. 따라서 회귀분석이 데이터를 잘 설명하는 경우는 아닙니다.
B - 데이터가 너무 퍼져있기 때문에 이 또한 회귀분석이 데이터를 잘 설명하는 경우가 아닙니다.
C - 선형으로 이루어져있기는 하지만, 하나의 선이 아니라 두개의 선으로 설명됩니다. 즉, 두개의 회귀분석 모델이 필요해보입니다.
D - A와 반대로 여러 X값에 대응되는 Y값은 하나입니다. 회귀선이 하나의 Y값만 예측하면 되기 때문에 회귀분석으로 설명하기 적절한 데이터입니다.
E - 데이터가 Y=aX+b인 선형이 아니라 Y=X2인 이차함수 형태로 설명됩니다.
이를 통해 이야기하고 싶은 것은, 수치를 통해 모델을 평가하는 것 뿐 아니라 시각화를 통해 데이터가 선형관계를 이루고 있는지도 볼 필요가 있다는 것이라고 생각했습니다. 회귀분석에서만이 아니라 데이터가 우리가 선택한 모델을 사용하기에 적절한 형태인지를 확인할 필요가 있는 것임을 의미합니다.
'강의정리 > udacity - machine learning' 카테고리의 다른 글
| Intro to machine learning - (8) Clustering (0) | 2021.01.19 |
|---|---|
| Intro to machine learning - (7) Outliers (0) | 2021.01.18 |
| Intro to machine learning - (6) Regression(1) (0) | 2021.01.13 |
| Intro to machine learning - (5) Datasets and Questions (0) | 2021.01.11 |
| Intro to machine learning - (4) Choose your own algorithm (0) | 2020.11.30 |




