| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 한빛미디어
- feature scaling
- regression
- 주피터테마
- 모두를 위한 딥러닝
- 주피터노트북
- deep learning
- 주피터노트북 커널 목록
- Python
- Git
- pandas
- 주피터노트북 커널 추가
- Udacity
- jupytertheme
- deeplearning
- 딥러닝
- 경사하강법
- GitHub
- 회귀분석
- Linear Regression
- 데이터분석
- Machine Learning
- MySQL
- overfitting
- 나는리뷰어다2021
- 주피터 노트북 테마
- ubuntu
- random forest
- 주피터노트북 커널 제거
- lol api
- Today
- Total
유승훈
Intro to machine learning - (6) Regression(1) 본문
Intro to machine learning - (6) Regression(1)
seunghuni96 2021. 1. 13. 23:52이번 챕터는 회귀분석에 대한 내용입니다.
보충이 필요한 내용은 학교에서 들었던 회귀분석 강의 내용을 첨부했습니다.

이전 강의에서 배웠던 알고리즘들이 이산형 Y 문제를 푸는 것들이었습니다. 하지만 데이터로 푸는 문제가 Y를 이산형으로 가질수도 있습니다. 키, 몸무게, 집값 등등..
이산형 Y인 문제를 푸는 알고리즘들 중 회귀분석(Regression)이 있습니다. 간단하게 데이터를 가장 잘 설명하는 선을 긋는 알고리즘이라고 이야기 할 수 있습니다.

독립변수가 하나인 단순회귀분석은 Y=aX+b의 형태로 정의됩니다. 예시에서는 Y가 net worth, X가 Age가 됩니다.
기울기(Slope)인 a는 X의 변화에 따른 Y의 변화량을 의미합니다. a가 커질수록 X의 변화에 따른 Y의 변화량은 커지고, 반대로 a가 작아질수록 X의 변화에 따른 Y의 변화는 줄어듭니다.
우리는 모수, 그러니까 모회귀선을 알지 못하기 때문에, 과거의 데이터를 통해 a,b를 추정합니다. 이 추정하는 과정이 곧 데이터를 가장 잘 설명하는 선을 찾는 과정입니다.

실제 관측값인 Yi와 Y의 평균의 차이의 제곱합을 SST(Total Sum of Squares)라고 합니다.
그 중 회귀선으로 설명되는 변동을 SSR, 회귀선으로 설명되지 않는 변동을 SSE라고 합니다.
당연히 SST=SSR이 되는게 최고의 결과라고 할 수 있습니다. SSE=0인 경우죠. 하지만 이 모델은 실제로 활용되지는 않을 것 입니다. Overfitting의 문제가 있을 가능성이 높기 때문에, 미래의 데이터를 잘 예측할것이라고 보기는 어렵습니다.
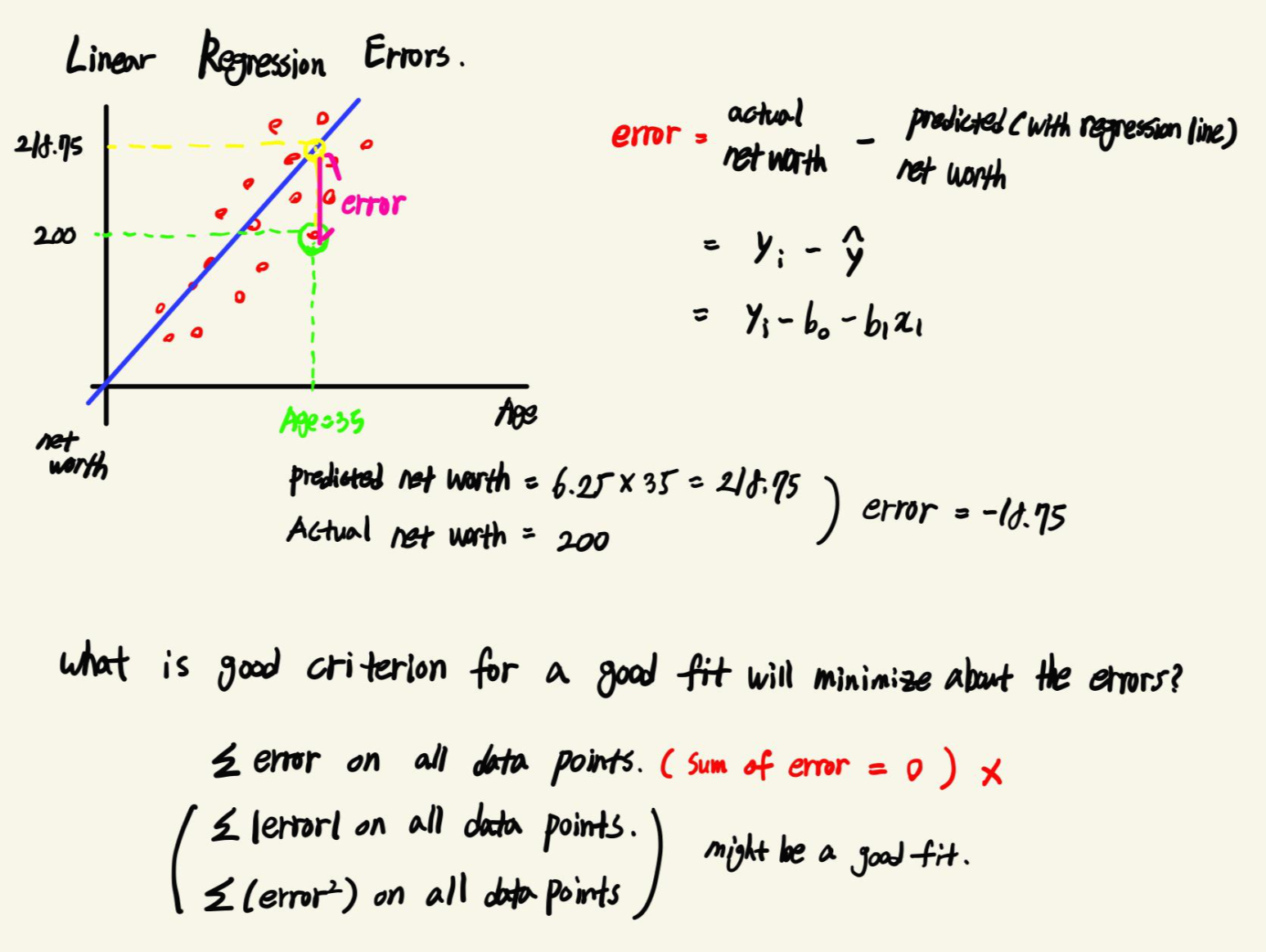
회귀선과 실제 데이터 사이의 거리가 회귀선의 Error입니다. 이 거리가 작을수록 에러가 적은, 즉 예측을 잘 하는 모델이라고 볼 수 있습니다. 그렇다면 Error를 최소화하는 좋은 기준은 무엇일까요?
- Error의 총합은 언제나 0이기 때문에 지표로 활용하기는 어렵습니다.
- Error의 절댓값의 총합이나, 제곱합이 좋은 선택지가 될 수 있을것 같네요.

앞서 얘기했듯, 우리의 목표는 실제 데이터와 회귀선의 예측값 사이의 거리, 즉 Error를 최소화 하는 것입니다.
Error를 최소화하는 회귀선을 구성하는 절편과 기울기를 찾는 것이죠. 최적해를 찾는 문제입니다. 크게 Ordinary Least Squares(OLS)라고 하는 최소제곱추정량과 Gradient Descent라고 하는 경사하강법을 쓸 수 있습니다. 회귀분석에서는 최소제곱추정량이 활용됩니다.

앞서 Error를 최소화하는 회귀선을 찾기 위해 오차 절댓값의 총합과 오차 제곱합을 최소화하는 것을 이야기했습니다. 하지만 실제 회귀분석에서는 오차 제곱합을 최소화하는 방법을 활용합니다.
강의에서는 오차 절댓값의 총합을 활용하지 않는 이유는, 이를 최소화하는 회귀선은 하나가 아니라 여러개가 존재할 수 있기 때문이라고 말합니다. 자세하게 이야기하면, 오차 절대값의 합은 연속적이지 않아서 미분이 불가능하기 때문에 Error를 줄여가면서 답을 찾는것이 힘들기 때문입니다. 계산이 어렵고, 해가 유일하지도 않을 수 있기 때문에 절대값의 합이 아는 제곱합을 활용하는 것입니다.
딥러닝 용어 정리, L1 Regularization, L2 Regularization 의 이해, 용도와 차이 설명
제가 공부하고 정리한 것을 나중에 다시 보기 위해 적는 글입니다. 제가 잘못 설명한 내용이 있다면 알려주시길 부탁드립니다. 사용된 이미지들의 출처는 본문에 링크로 나와 있거나 글의 가장
light-tree.tistory.com
해당 내용이 이 글에 상당히 정리가 잘 되어있어서 첨부했습니다. 위 내용을 이해하는데 필요한 것들을 정리하면,
Norm
- Norm은 벡터의 크기(혹은 길이)를 측정하는 방법(혹은 함수)입니다. 두 벡터 사이의 거리를 측정하는 방법이기도 합니다"
- L1 Norm은 두 벡터의 각 원소들의 차이의 절대값의 합입니다.
- L2 Norm은 두 벡터의 유클리디안 거리(직선 거리)입니다.
- L1 Norm은 여러가지 Path를 가지지만, L2 Norm은 Unique Shortest Path를 가집니다.
Loss
- L1 Loss는 실제값과 예측치 사이의 차이(오차)의 절대값을 구하고, 그 오차들의 합을 계산한 것입니다.
- L2 Loss는 오차의 제곱의 합으로 정의됩니다.
- L2 Loss는 직관적으로 오차의 제곱을 더하기 때문에 Outlier에 더 큰 영향을 받습니다. "L1 Loss가 L2 Loss에 비해 Outlier에 대하여 더 Robust(덜 민감 혹은 둔감)하다."라고 표현할 수 있습니다.
이렇게 오차 절대값의 총합과 제곱합의 차이를 어렵지 않게 이해할 수 있습니다.
일반적인 선형회귀분석에서 사용되는 것이 L2 Loss입니다. 하지만 "L2 Loss는 직관적으로 오차의 제곱을 더하기 때문에 Outlier에 더 큰 영향을 받습니다." 소수의 Outlier 때문에 추정이 왜곡될 수 있는 것입니다. 따라서 Outlier의 영향력을 줄인 회귀분석 모델을 사용하고자 하는 경우에는 L2 Loss대신 L1 Loss를 최소화하는 Robust Regression을 활용할 수 있습니다.
이렇게 도출된 회귀분석은 사실 언제나 쓰일 수 있는 것은 아닙니다. 몇가지 기본 조건을 만족해야 활용 가능한 추정량이 됩니다. 이 정리를 Gauss-Markov Theorm. 가우스-마코프 정리라고 합니다.
1. 회귀모형은 선형모형이다.
2. 오차항의 기대값은 0이다.
3. 오차항은 등분산성을 갖는다.
4. 모든 오차항은 독립이다.
5. x는 확률변수가 아니다.
6. (옵션) 오차항은 정규분포를 따른다.
"위의 1-5의 가정을 만족할 때, 최소제곱법을 통해 추정된 기울기와 절편이 최고의 선형 불편추정량(Best Linear Unbiased Estimator : BLUE)을 갖는다."
다음 글로 이어집니다.
'강의정리 > udacity - machine learning' 카테고리의 다른 글
| Intro to machine learning - (7) Outliers (0) | 2021.01.18 |
|---|---|
| Intro to machine learning - (6) Regression(2) (0) | 2021.01.15 |
| Intro to machine learning - (5) Datasets and Questions (0) | 2021.01.11 |
| Intro to machine learning - (4) Choose your own algorithm (0) | 2020.11.30 |
| Intro to machine learning - (3) Decision Tree (0) | 2020.11.17 |




