Intro to machine learning - (12) PCA

seunghunii/tistory_codes

이번 글에서는 PCA에 대해서 소개하고 있습니다.

PCA는 기존 데이터의 좌표계를 기반으로 새로운 좌표계를 만들어냅니다. 원 좌표계의 원점을 우리가 가진 데이터의 중심으로 바꿉니다. 그리고 X축을 분산의 주축으로 바꿉니다. 이 축은 각 Data들과의 거리가 가장 적습니다. 그리고 Y축을 그와 직교하며 그 다음으로 분산이 큰 방향으로 설정합니다.

 

PCA는 이 축들을 찾고, 이 축들이 얼마나 중요한지를 말해줍니다.

 

이 데이터에서 새로운 원점을 찾으면, (2,3)이 됩니다. 이를 기반으로  두 벡터의 성분을 찾으면, $X{}'$는 (1,1), $Y{}'$는 (-1,1)이 됩니다. 두 벡터가 직교하기 때문에, 두 벡터의 내적은 0이 됩니다. 

 

중요성을 따지면, 분산이 가장 큰 $X{}'$가 가장 중요한 변수가 되고, 그 다음으로 분산이 큰 $Y{}'$가 중요한 변수가 됩니다. 

 

세 가지 경우의 데이터가 있습니다. PCA를 돌려서 세개의 데이터 모두 결과를 얻을 수는 있습니다.

 

하지만 A,C와는 다르게 B는 새로 만들어진 `X`,`Y`사이의 분산 차이가 크게 나지 않는 것 같습니다. 이런 상황에서는 두 벡터의 고유값도 비슷하고, PCA를 통해 얻는 것이 크게 없어보입니다. 

 

집의 가격을 예측하는 문제를 풀고 있다고 합시다. 우리가 측정 가능한것들로는 집의 평수, 방의 개수, 학교의 순위, 동네의 안전함이 있습니다. 이를 기반으로 잠재변수인 집의 크기와 이웃이라는 변수를 관측하고자 합니다.

 

집의 평수와 방의 개수로 집의 크기를 볼 수 있고, 학교의 순위와 동네의 안전함으로 이웃 변수를 관측할 수 있습니다.

 

4개의 변수를 2개로 응축하는 방법은 무엇이 있을까요? Feature Selection의 관점으로 생각해보면 Scikit-Learn의 SelectKBest와 SelectPercentile을 사용할 수 있습니다. KBest는 가장 좋은 K개의 변수를 Percentile은 전체 변수 중 입력한 비율만큼의 변수를 남깁니다. 여기에서는 집의 크기와 이웃이라는 두개의 변수를 최종적으로 활용하는 것이 정해져있으니, Percentile보다는 KBest가 더 알맞습니다.

 

이것이 PCA의 기본개념입니다.

 

내가 여러 변수를 가지고 있는데, 가진 것 보다 적은 개수의 변수로 데이터의 패턴을 설명할 수 있다고 가정하면, 변수들을 응축해서 기저의 현상을 더 잘 설명할 수 있도록 하는 것입니다.

 

여기서 응축된 변수들이 Principle Component라고 하는 주성분입니다.

 

응축하는 과정을 간단하게 설명하면, 두 변수 사이의 Principle Component를 긋고, 각 Data를 투영합니다. 그러면 Data들이 Principle Component위에 투영되면서 2차원이었던 데이터가 1차원이 됩니다. 이렇게 집의 평수와 방의 개수를 응축해서 집의 크기를 나타내는 변수로 만들 수 있습니다.

 

이러한 Principle Component를 결정하는 것은 Variance입니다. "데이터가 퍼진 정도"를 의미합니다. Principle Component는 분산이 가장 큰 방향으로 정하는데, 분산이 가장 크다는 것은 기존 데이터의 정보를 가장 많이 가지고 있다는 것을 의미하기 때문입니다.

 

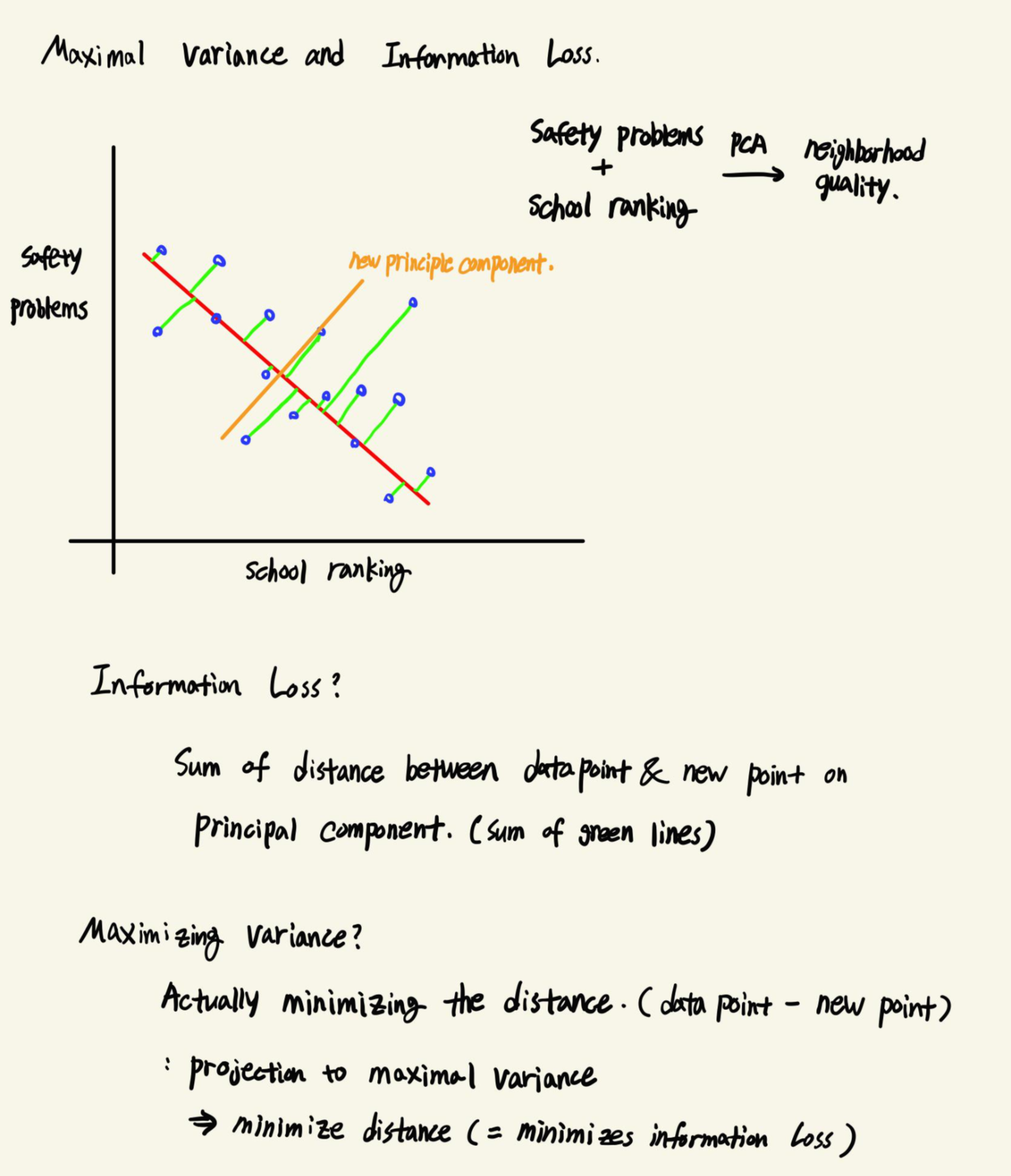
기존 데이터의 정보를 가장 많이 가지고 있다는 것은, 2차원 데이터를 1차원 데이터로 변환하면서 잃게 되는 정보의 양이 가정 적다는 것을 의미합니다. 여기서 말하는 정보의 양은, 기존 데이터와 투영을 통해 만들어진 새로운 데이터 사이의 거리입니다. 기존의 데이터와 새로운 데이터 사이의 거리가 멀수록 많은 정보를 잃게 되는 것입니다.

 

이와 직교하는 새로운 Principle Component인 Orange Line을 보면, Information Loss가 Red Line보다 더 커보입니다. 각각의 데이터 모두에 해당하는 것이 아니라, 거리를 합해서 비교했을때를 의미합니다. 

 

여기서 분산을 Maximize하는 것은, 기존 데이터와 투용을 통해 만들어진 데이터 사이의 거리를 최소화하는 것입니다. 최대 분산으로 기존의 데이터를 투영함을 통해 새로운 데이터를 만드는 것은, 거리를 최소화하고, 데이터의 차원이 고차원에서 저차원으로 가면서 잃게되는 정보의 양을 최소화하는 것이기도 합니다.

 

집의 가격을 예측하는 문제에서, 우리는 4개의 변수를 임의로 묶어서 집의 크기와 이웃 2개의 변수로 만들었습니다. 변수를 묶을때 우리는 사람의 직관을 사용했습니다. 하지만 언제나 이렇게 묶을 수 있는 것은 아닙니다. 얼굴인식을 예로 들면, 셀수없이 많은 Pixel들로 이루어져 있는데, 이 Feature들을 직관적으로 묶는 것은 불가능하기 떄문입니다.

 

그래서 보통은, 모든 Feature를 PCA에 넣으면, PCA가 자동으로 묶고, 상대적인 영향력을 측정합니다. 이에 따라서 PCA로 만들어지는 변수가 어떤 Latent Feature인지를 판단할 수 있습니다.

 

정리를 하면,

• PCA는 입력변수들을 주성분으로 변환할 수 있는 방법이다.

• 이렇게 변환된 주성분들을 입력변수로서 쓸 수 있다.

• 주성분은 투영할때 분산을 최대화(=정보의 손실을 최소화하는)하는 방향으로 이루어진다.

• 주성분에서의 분산이 클수록, 그 주성분은 높은 순위에 오른다.

• 가장 분산이 크고 / 정보의 양이 많은 성분이 첫번째 성분이 되고, 그 다음으로 분산이 크면서 첫번째 성분과 겹치지 않는 성분이 두번째 성분이 된다.

• 주성분의 최대치는 입력변수의 숫자이다. 보통은 적은 수의 주성분을 사용하지만, 입력변수 숫자만큼의 주성분을 쓸수도 있다. 하지만 이때는 PCA로 얻는 효과가 없다.

PCA가 쓰이는 상황으로는

• 아직 드러나지 않은 데이터의 잠재변수를 활용하고자 할 때

• 차원축소

  • 고차원의 데이터를 시각화

  • Noise 감소(후순위의 Component를 사용하지 않음으로서 Noise 감소)

  • 다른 알고리즘(회귀, 분류)이 더 좋은 성능을 보이도록 함.